USE CASE |
|
| Title: | Disambiguating KBpedia Knowledge Graph Concepts |
| Short Description: | This use case describes a fast method for disambiguating concepts, when more than one possible match is provided. |
| Problem: | When "tagging" or extracting concepts, most methods rely on matching the surface forms of the names or labels associated with the concepts. However, these specific terms or phrases may be, in themselves, ambiguous; that is, they may match to multiple possible concepts (think of words like "bank", "club", "fan", "right", etc.). Thus, the proper meaning of a term or phrase depends on its use and context. Disambiguation methods must make these discriminations. |
| Approach: | The KBpedia knowledge graph is based on consistent and coherent relationships. Related concepts are located close to one another; unrelated concepts reside much farther apart in the graph. Graph embeddings for each node and its adjacent neighbors in the graph are created using the DeepWalk method, which creates a vector for each concept. Surface forms of matching concepts are first obtained via fairly straightforward parsing. Where potential matches have more than one candidate concept, its vector representation is compared to vectors from the surrounding text; most closely aligned vectors are taken as the most accurate match, thus disambiguating from amongst the ambiguous candidates. Simple linear algebra equations are used to make these comparison calculations, a process that is extremely fast. The overall process is captured by a repeatable pipeline with statistical reporting, enabling rapid refinements in parameters and methods to achieve the best-performing model. This general method can be applied to entities as well as concepts. |
| Key Findings |
|
One of the most important natural language processing tasks is to "tag" concepts in text. Tagging a concept means determining whether words or phrases in a text document match any of the concepts that exist in a knowledge structure (such as a knowledge graph, an ontology, a taxonomy, a vocabulary, etc.). (BTW, a similar definition and process applies to tagging an entity.) What is usually performed when tagging is that the input text is parsed and normalized in some manner. Then all of the surface forms of the concepts within the input knowledge structure (based on their preferred and alternative labels) are matched against the words within the text. "Tagging" is when a match occurs between a concept in the knowledge structure and one of its surface forms in the input text.
But here is the problem. Given the ambiguous world we live in, often this surface form, which after all is only a word or phrase, may be associated with multiple different concepts. When we identify the surface form of "bank", does that term refer to a financial institution, the shore of a river, a plane turning, or a pool shot? Identical surface forms may refer to totally different concepts. Further, sometimes a single concept will be identified but it won't be the right concept, possibly because the right one is missing from the knowledge structure or other issues.
The purpose of this article is thus to explain how we can "disambiguate" (that is, suggest the proper concept from an ambiguous list) the concepts that have been tagged. What we will do is to show how we can leverage the KBpedia knowledge graph structure as-is to perform this disambiguation. What we will do is to create graph embeddings for each of the KBpedia concepts using the DeepWalk algorithm. Then we will perform simple linear algebra equations on the graph embeddings to determine if the tagged concept(s) is the right one given its context or not. We will test multiple different algorithms and strategies to analyze the impact on the overall disambiguation performance of the system.
Different Situations
Before starting to work on the problem, let's discuss the issues we may encounter with any tagging and disambiguation task. The three possibilities we may encounter are:
- A word in the text refers to a concept, but the concept hasn't been identified (is not in the graph)
- A word in the text has been tagged with a single concept, but that concept is not the right one (the right one is not in the graph)
- A word in the text has been tagged with multiple concepts, so the right concept needs to be selected amongst the options offered.
What we present in this article is how we can automatically disambiguate the situations 2 and 3. (To fix the first situation, not addressed further herein, we would have to add additional surface forms to the knowledge graph by adding new alternative labels to existing concepts, or by adding new concepts with their own surface forms.)
Disambiguation Process
The disambiguation process is composed of two main tasks: the creation of the graph embeddings for each concept in the KBpedia knowledge graph, and then the evaluation of each tagged concept to disambiguate them.
Introducing DeepWalk
DeepWalk was created to learn social representations of a graph's vertices that capture neighborhood similarity and community membership. DeepWalk generalizes neural language models to process a special language composed of a set of randomly-generated walks.
We want to use DeepWalk not to learn social representations but to learn the relationship (that is, the similarity) between all of the concepts existing in a knowledge graph given different kinds of relationships such as sub-class-of, super-class-of, equivalent-class or other relationships such as KBpedia's 80 aspects relationships. (Note, we also discussed and used DeepWalk in another use case extending KBpedia.)
For this use case we use the DeepWalk algorithm to select concepts from the broader Wikipedia corpus. Other tasks that could be performed using DeepWalk in a similar manner are:
- Content recommendation,
- Anomaly detection [in the knowledge graph], or
- Missing link prediction [in the knowledge graph].
Note that we randomly walk the graphs as stated in DeepWalk's original paper 1. However more experiments could be performed to change the random walk by other graph walk strategies like depth-first or breadth-first walks.
Create Graph Embedding Vectors
We first create a graph embedding for each of the Wikipedia categories. What we have to do is to use the Wikipedia category structure along with the linked KBpedia knowledge graph. Then we have to generate the graph embedding for each of the Wikipedia categories that exist in the structure.
The graph embeddings are generated using the DeepWalk algorithm over that linked structure. It randomly walks the linked graph hundred of times to generate the graph embeddings for each category.
Create Deeplearning4j Graph
To generate the graph embeddings, we use Deeplearning4j's DeepWalk implementation. This step creates a Deeplearning4j graph structure that is used by its DeepWalk implementation to generate the embeddings.
The graph we have to create is composed of the latest version of KBpedia knowledge graph version 1.20. Since the only concepts we want to disambiguate are the KBpedia reference concepts as tagged by the tagger, then this is the only knowledge structure we have to load to create the graph embeddings.
Then we generate the initial Deeplearning4j graph structure composed of the inferred KBpedia knowledge graph.
(use '[cognonto-deepwalk.core]) (require '[clojure.string :as string]) (require '[clojure.data.csv :as csv]) (require '[clojure.java.io :as io]) (require '[cognonto-owl.query :as query]) (defonce knowledge-graph (load-knowledge-graph "file:/d:/cognonto-git/kbpedia-generator/kbpedia/1.10/target/kbpedia_reference_concepts_linkage_inferrence_extended_2.n3.owl"))
Train DeepWalk
Once the Deeplearning4j graph is created, the next step is to create and train the DeepWalk algorithm. What the (create-deep-walk) function does is to create and initialize a DeepWalk object with the Graph we created above and with some hyperparameters.
The :window-size hyperparameter is the size of the window used by the continuous Skip-gram algorithm used in DeepWalk. The :vector-size hyperparameter is the size of the embedding vectors we want the DeepWalk to generate (it is the number of dimensions of our model). The :learning-rate is the initial leaning rate of the Stochastic gradient descent.
For this task, we initially use a window of 15 and 3 dimensions to make visualizations simpler to interpret, and an initial learning rate of 2.5%.
(def graph (create-deepwalk-graph knowledge-graph :directed? true)) (def deep-walk (create-deep-walk graph :window-size 15 :vector-size 3 :learning-rate 0.025))
Once the DeepWalk object is created and initialized with the graph, the next step is to train that model to generate the embedding vectors for each vertex in the graph.
The training is performed using a random walk iterator. The two hyperparameters related to the training process are the walk-length and the walks-per-vertex. The walk-length is the number of vertices we want to visit for each iteration. The walks-per-vertex is the number of timex we want to create random walks for each vertex in the graph.
(defn train ([deep-walk iterator] (train deep-walk iterator 1)) ([deep-walk iterator walks-per-vertex] (.fit deep-walk iterator) (dotimes [n walks-per-vertex] (.reset iterator) (.fit deep-walk iterator))) ([deep-walk graph walk-length walks-per-vertex] (train deep-walk (new RandomWalkIterator graph walk-length) walks-per-vertex)))
For the initial setup, we want to have a walk-length of 15 and we want to iterate the process 175 times per vertex.
(train deep-walk graph 15 175)
Concept Disambiguation
Now that all of the KBpedia reference concepts are characterized using the graph embeddings, how can we disambiguate each of these concepts in a text? The first thing is to observe what is happening. When we tag a sentence such as "A sandstorm blows over damaged buildings in rebel held area of Douma." the first step that happens is that the surface forms (preferred labels and alternative labels) of the KBpedia concepts are identified within the sentence. As we discussed above, it is possible that a word, or a group of words, may get tagged with multiple KBpedia reference concepts.
Because we characterized each of the concepts with its graph embeddings, it means that what we are dealing with is a series of vectors that represent the "meaning" of each concept in the knowledge graph structure. What we end-up with is the following:
The next step is to use that information to try to disambiguate each of these concepts. To try to disambiguate the concepts, we have to make a few assumptions. First we have to assume that the graph embeddings created by the DeepWalk algorithm when crawling the KBpedia knowledge graph represent the "meaning" of the concept within the knowledge structure. Then we have to assume that the sentence where the concept has been identified creates a context that we can use to disambiguate the identified concepts based on their "meaning".
In the example above, the context is the sentence, and four concepts have been identified. The big assumption we are making here is that each identified concept is "tightly" related to others in the knowledge graph. Given this assumption, what we have to do is to calculate the relatedness of each concept, within the context, and keep the ones that are closest to each other.
Gold Standard Creation
Before digging into how we will perform the disambiguation of these concepts, another step is to create a gold standard that we will use to evaluate the performance of our model and to check the impact of different hyperparameters on the disambiguation process. We created this gold standard manually by using random sentences found in online news articles. We first tagged each of these sentences using the tagger. Then, we manually disambiguated each of the tagged concepts. This gives us the properly labeled training set for our exercise. The result is the following gold standard file.
Each of the annotations looks like this:
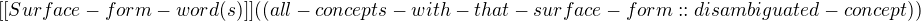
This markup first presents the surface forms for the related concept(s) in the knowledge graph within the double brackets, followed by the concept(s) URI endings between the double parenthesis. The double colon :: designator provides the suggested disambiguated concept. If nothing follows the double colon it means that the correct concept does not exist in the knowledge graph).
Disambiguation Method
The actual disambiguation method is based on some simple linear algebra formulas.
Each tagged word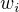 
is related to a sliding context 
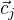where 
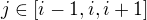. Each tagged word has 
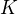graph embedding vectors (i.e. a "sense" vector) 
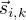where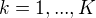 
. What we want the disambiguation method to do is to calculate a score between each embedding vector of each identified concept of each word given its sliding context. The score is calculated by performing the dot product between the graph embedding vector 
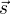and the sliding context vector 
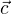. The sliding context vector is calculated by summing the graph embedding vector 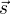of each word 
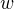within the window:
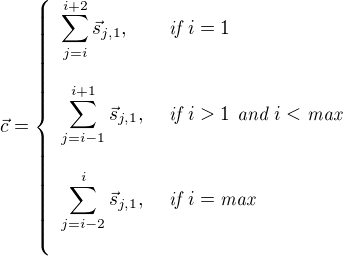
Finally the score is calculated using:
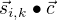
This is the first definition of the score we want to use to begin to disambiguate concepts from the knowledge graph associated with words in a sentence. As you can read from the formula, only the first sense for each word 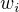is being selected for each word within the sliding window that creates the context. (Other variants are be explored later in this article.) However as we will see below, we will change that formulas a bit such that the score becomes easier to understand for a human by expressing it in degrees. What is important to understand here is that we use two vectors to calculate the score: the graph embedding of the concept we want to disambiguate and the vector calculated from the windowed context that sums all the graph embedding vectors of each concept within that window.
Now let's put this method into code. The first thing we have to do is to create a lookup table that is composed of the graph embeddings for each of the concepts that exist in the KBpedia knowledge graph as we calculated with the DeepWalk algorithm above.
(def index (->> (query/get-classes knowledge-graph) (map-indexed (fn [i class] (if-not (string? class) {(.toString (.getIRI class)) (inc i)} {class (inc i)}))) (apply merge))) (def ^:dynamic vertex-vectors (.getVertexVectors (.lookupTable deep-walk)))
Getting the vector 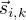for the word 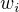is as simple as getting it from the lookup table we created above:
(defn get-vector [uri-ending] (when-let [concept (get index (str "http://kbpedia.org/kko/rc/" uri-ending))] (.getRow vertex-vectors concept)))
To get the sense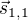 
of the word 
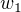(which is SandstormAsObject) in our example sentence above, we only have to:
(.toString (.data (get-vector "SandstormAsObject")))
[0.08586349,-0.06854561,-0.14704005]
To get the vector 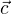of the context of the word 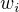we have to do some more work. We have to create a function that will calculate the dot product between two vectors. Then we will have to create another function that will calculate the sum of x number of vectors.
(defn dot-product-clj [x y] (->> (interleave x y) (partition 2 2) (map #(apply * %)) (reduce +))) (defn angle-clj [a b] (Math/toDegrees (Math/acos (/ (dot-product-clj a b) (* (Math/sqrt (dot-product-clj a a)) (Math/sqrt (dot-product-clj b b))))))) (defn disambiguate [line] (let [tags (re-seq #"\[\[(.*?)\]\]\(\((.*?)\)\)" line)] (clojure.pprint/pprint tags) (println) (loop [i 0 tag (first tags) rtags (rest tags)] (let [word (second tag) concepts (last tag) concept (get-tag-concept concepts)] (println word " --> " concepts) ;; Disambiguate concepts (let [ambiguous-concepts (string/split (first (string/split concepts #"::")) #" ")] (doseq [ambiguous-concept ambiguous-concepts] (println "a-vector: " (get-vector ambiguous-concept)) (println "b-vector: " (get-context i tags)) (println "dot product: " (dot-product (get-vector ambiguous-concept) (get-context i tags))) (println "angle: " (angle (get-vector ambiguous-concept) (get-context i tags))) (println))) (when-not (empty? rtags) (recur (inc i) (first rtags) (rest rtags)))))))
(defn dot-product "Calculate the dot product of two vectors (NDArray)" [v1 v2] (first (read-string (.toString (.data (.mmul v1 (.transpose v2))))))) (defn sum-vectors "Sum any number of vectors (NDArray)" [& args] (let [args (remove nil? args)] (loop [result (first args) args (rest args)] (if (empty? args) result (recur (.add result (first args)) (rest args))))))
The next step is to create the function that calculates the context vector, which is a sliding window of the concept associated with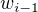 
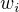, and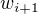 
.
(defn get-tag-concept [concepts] (if (> (.indexOf concepts "::") -1) (second (re-find #"::(.*)" concepts)) concepts))
Let's see how that works. To calculate 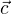when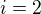 
we have to calculate 
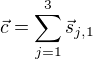which can be done with the following code:
;; s{1,1} (def sandstormasobject (get-vector "SandstormAsObject")) ;; s{2,1} (def blowingair (get-vector "BlowingAir")) ;; s{3,1} (def building (get-vector "Building")) (def c (sum-vectors sandstormasobject blowingair building)) (println (.toString (.data c)))
[0.24941699,-0.0940429,-0.11848262]
Finally we have to calculate the score used to disambiguate the two senses of the word blows by performing the dot product between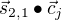 
and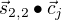 
where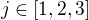 
which can be done using the following code:
;; s{2,2} (def windprocess (get-vector "WindProcess")) (println "BlowingAir score:" (dot-product blowingair c)) (println "WindProcess score:" (dot-product windprocess c))
BlowingAir score: 0.011248392
WindProcess score: 0.005993685
What the scores suggest is, given the context, the right concept associated with the word blows is BlowingAir since its score is bigger. This is the right answer. We can see how simple linear algebra manipulations can be used to help us automatically disambiguate such concepts. In fact, the crux of the problem is not to perform these operations but to create a coherent and consistent knowledge graph such as KBpedia and then to create the right graph embeddings for each of its concepts. The coherent graph structure gives us this disambiguation capability for "free".
However, these scores, as is, are hard to interpret and understand. What we want to do next is to transform these numbers into a degree between 0 and 360. The degree between the word sense's vector 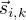and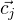 
represent how close the two vectors are to each other. A degree 0 would means that both vectors are identical in terms of relationship, and a degree of 180 would mean they are quite dissimilar. What we will see later is that we can use scores such as this to drop senses that score above some similarity degree threshold.
The angle between the two vectors can easily be calculated with the following formula:
The following code will calculate the angle between two vectors using this formula:
(defn angle [a b] (Math/toDegrees (Math/acos (/ (dot-product a b) (* (Math/sqrt (dot-product a a)) (Math/sqrt (dot-product b b)))))))
OK, so let's get the angle between the example we created above:
(println "BlowingAir degree score:" (angle blowingair c)) (println "WindProcess degree score:" (angle windprocess c))
BlowingAir degree score: 76.77807342393672
WindProcess degree score: 82.80469144165336
Since the degree between the context and BlowingAir is smaller than the degree between the context and WindProcess, we keep the word blows as the disambiguated concept.
Evaluate Model
The last step is to evaluate the model we created. What we have to do is to create a function called (evaluate-disambiguation-model) that will read the gold standard file, parse the markup and then perform the disambiguation. Then the precision, recall, acuracy and F1 metrics will be calculated to get the performance of this disambiguation system and the models we created for it.
(defn get-first-sense-vector [concepts] (get-vector (if (> (.indexOf concepts "::") -1) (first (string/split (second (re-find #"(.*)::" concepts)) #" ")) concepts))) (defn get-context [i tags] (if (= (count tags) 1) ;; There is only one tag in the sentence (get-first-sense-vector (last (first tags))) (if (= (count tags) 2) ;; There is only 2 tags in the sentence (sum-vectors (get-first-sense-vector (last (first tags))) (get-first-sense-vector (last (second tags)))) ;; Target concept is the first one of the sentence (if (= i 0) (sum-vectors (get-first-sense-vector (last (first tags))) (get-first-sense-vector (last (second tags))) (get-first-sense-vector (last (nth tags (+ i 2))))) ;; Target concept is the last one of the sentence (if (= i (- (count tags) 1)) (sum-vectors (get-first-sense-vector (last (nth tags (- i 2)))) (get-first-sense-vector (last (nth tags (- i 1)))) (get-first-sense-vector (last (nth tags i)))) ;; Target is in-between (sum-vectors (get-first-sense-vector (last (nth tags (- i 1)))) (get-first-sense-vector (last (nth tags i))) (get-first-sense-vector (last (nth tags (+ i 1)))))))))) (defn predict-label [ambiguous-concepts i tags max-angle] (second (first (->> ambiguous-concepts (map (fn [ambiguous-concept] (if-let [a (get-vector ambiguous-concept)] (if-let [b (get-context i tags)] (if (> (angle a b) max-angle) {} {(angle a b) ambiguous-concept}) {}) {}))) (apply merge) sort)))) (defn predict-label-angle [ambiguous-concepts i tags] (first (->> ambiguous-concepts (map (fn [ambiguous-concept] (if-let [a (get-vector ambiguous-concept)] (if-let [b (get-context i tags)] {(angle a b) ambiguous-concept}) {}))) (apply merge) sort))) (defn evaluate-disambiguation-model [gold-standard-file & {:keys [max-angle] :or {max-angle 90.0}}] (let [sentences (with-open [in-file (io/reader gold-standard-file)] (doall (csv/read-csv in-file :separator \tab))) true-positive (atom 0) false-positive (atom 0) true-negative (atom 0) false-negative (atom 0)] (doseq [[sentence] sentences] (let [tags (re-seq #"\[\[(.*?)\]\]\(\((.*?)\)\)" sentence)] (loop [i 0 tag (first tags) rtags (rest tags)] (when-not (= i (count tags)) ;; Disambiguate concepts (let [word (second tag) concepts (last tag) concept (get-tag-concept concepts) label (second (re-find #"::(.*)" concepts)) ambiguous-concepts (string/split (first (string/split concepts #"::")) #" ") predicted-label (predict-label ambiguous-concepts i tags max-angle)] (when (and (= label predicted-label) (not (empty? label)) (not (empty? predicted-label))) (swap! true-positive inc)) (when (and (not (= label predicted-label)) (not (empty? predicted-label))) (swap! false-positive inc)) (when (and (empty? label) (empty? predicted-label)) (swap! true-negative inc)) (when (and (not (empty? label)) (empty? predicted-label)) (swap! false-negative inc)) (recur (inc i) (first rtags) (rest rtags))))))) (println "True positive: " @true-positive) (println "false positive: " @false-positive) (println "True negative: " @true-negative) (println "False negative: " @false-negative) (println) (if (= 0 @true-positive) (let [precision 0 recall 0 accuracy 0 f1 0] (println "Precision: " precision) (println "Recall: " recall) (println "Accuracy: " accuracy) (println "F1: " f1) {:precision precision :recall recall :accuracy accuracy :f1 f1}) (let [precision (float (/ @true-positive (+ @true-positive @false-positive))) recall (float (/ @true-positive (+ @true-positive @false-negative))) accuracy (float (/ (+ @true-positive @true-negative) (+ @true-positive @false-negative @false-positive @true-negative))) f1 (float (* 2 (/ (* precision recall) (+ precision recall))))] (println "Precision: " precision) (println "Recall: " recall) (println "Accuracy: " accuracy) (println "F1: " f1) {:precision precision :recall recall :accuracy accuracy :f1 f1}))))
Evaluation Baseline: Random Sense
Before evaluating the initial model we described above, the first thing we should be doing is to check the result of each metric we want to evaluate if we take a concept at random. To do this, we will modify the (evaluate-disambiguation-model) function we created above to perform the selection of the "disambiguated" sense at random. This will provide the baseline to evaluate the other algorithms we will test.
(defn evaluate-disambiguation-model-random [gold-standard-file & {:keys [max-angle] :or {max-angle 90.0}}] (let [sentences (with-open [in-file (io/reader gold-standard-file)] (doall (csv/read-csv in-file :separator \tab))) true-positive (atom 0) false-positive (atom 0) true-negative (atom 0) false-negative (atom 0)] (doseq [[sentence] sentences] (let [tags (re-seq #"\[\[(.*?)\]\]\(\((.*?)\)\)" sentence)] (loop [i 0 tag (first tags) rtags (rest tags)] (when-not (= i (count tags)) ;; Disambiguate concepts (let [word (second tag) concepts (last tag) concept (get-tag-concept concepts) label (second (re-find #"::(.*)" concepts)) ambiguous-concepts (string/split (first (string/split concepts #"::")) #" ") predicted-label (rand-nth (into ambiguous-concepts [nil]))] (when (and (= label predicted-label) (not (empty? label)) (not (empty? predicted-label))) (swap! true-positive inc)) (when (and (not (= label predicted-label)) (not (empty? predicted-label))) (swap! false-positive inc)) (when (and (empty? label) (empty? predicted-label)) (swap! true-negative inc)) (when (and (not (empty? label)) (empty? predicted-label)) (swap! false-negative inc)) (recur (inc i) (first rtags) (rest rtags))))))) (if (= 0 @true-positive) (let [precision 0 recall 0 accuracy 0 f1 0] {:precision precision :recall recall :accuracy accuracy :f1 f1}) (let [precision (float (/ @true-positive (+ @true-positive @false-positive))) recall (float (/ @true-positive (+ @true-positive @false-negative))) accuracy (float (/ (+ @true-positive @true-negative) (+ @true-positive @false-negative @false-positive @true-negative))) f1 (float (* 2 (/ (* precision recall) (+ precision recall))))] {:precision precision :recall recall :accuracy accuracy :f1 f1}))))
What we do is to calculate the average random sense disambiguation score for each metric. We run the (evaluate-disambiguation-model-random) one thousand times and then calculate the average.
(let [f1 (atom 0) precision (atom 0) accuracy (atom 0) recall (atom 0) nb (atom 0)] (dotimes [i 1000] (let [results (evaluate-disambiguation-model-random "resources/disambiguation-gold.standard.csv")] (swap! nb inc) (swap! f1 + (:f1 results)) (swap! precision + (:precision results)) (swap! recall + (:recall results)) (swap! accuracy + (:accuracy results)))) (println "Average precision: " (/ @precision @nb)) (println "Average recall: " (/ @recall @nb)) (println "Average accuracy: " (/ @accuracy @nb)) (println "Average F1: " (/ @f1 @nb)))
Average precision: 0.6080861368775368
Average recall: 0.49945064118504523
Average accuracy: 0.42075299778580666
Average F1: 0.5480979214012622
This gives us a baseline precision score of 0.608, recall score of 0.499, accuracy score of 0.420 and F1 score of 0.548.
Evaluation: First Sense Context
Now that we have our baseline in place, let's see the performance of the initial first-sensse-context disambiguation algorithm as described above compared to a random process. Note that this initial run is using an unoptimized DeepWalk graph with initial general hyperparameters.
(evaluate-disambiguation-model "resources/disambiguation-gold.standard.csv")
True positive: 246
false positive: 126
True negative: 9
False negative: 36
Precision: 0.66129035
Recall: 0.87234044
Accuracy: 0.6115108
F1: 0.7522936
As you can see, even using unoptimized default hyperparameters, we calculate an F1 score of 0.752, which is an increase of 37.26% over the baseline. Other measures improve, too: Recall (increased by 74.67%), accuracy (increased by 45.35%) and precision (increased by 8.75%).
We properly identified 246 of 417 examples. 126 were wrongly identified, 9 were properly discarded and 36 have been discarded when they shouldn't.
These results are really promising, but can we do better?
Hyperparameter Optimization
Now that we have a disambiguation workflow in place with standards by which to compute performance statistics, the final step is to try to optimize the system by testing multiple different values for some of the hyperparameters that can impact the performance of the system. The parameters we want to optimize are the:
- Size of the DeepWalk vectors
- Window size of the skip-gram
- Depth of the walks
- Number of iterations per concept, and the
- Angle threshold
Then we will perform a grid search to find the optimal hyperparameters to try to optimize each of the metric.
(defn svm-grid-search [graph & {:keys [grid-parameters] :or {grid-parameters {:window-size [10 15] :vector-size [3 16 64 128 256 512] :walk-length [5 10 15] :walks-per-vertex [32 64 128 256] :angle [30 60 90 120] :selection-metrics [:precision :accuracy :recall :f1]}}}] (let [best (atom (->> (:selection-metrics grid-parameters) (map (fn [selection-metric] {selection-metric {:window-size nil :vector-size nil :walk-length nil :walks-per-vertex nil :angle nil :score 0.0}})) (apply merge))) parameters grid-parameters] (doseq [window-size (:window-size parameters)] (doseq [vector-size (:vector-size parameters)] (let [deep-walk (create-deep-walk graph :window-size window-size :vector-size vector-size :learning-rate 0.025)] (doseq [walk-length (:walk-length parameters)] (doseq [walks-per-vertex (:walks-per-vertex parameters)] (train deep-walk graph walk-length walks-per-vertex) (doseq [angle (:angle parameters)] (let [results (binding [vertex-vectors (.getVertexVectors (.lookupTable deep-walk))] (evaluate-disambiguation-model "resources/disambiguation-gold.standard.csv" :max-angle angle))] (doseq [selection-metric (:selection-metrics parameters)] (let [score (get results selection-metric)] (println) (println "Window size: " window-size) (println "Vector size: " vector-size) (println "Walk length: " walk-length) (println "Walks per vertex: " walks-per-vertex) (println "Angle: " angle) (println "Score ("selection-metric"): " score) (println) (println) (when (> score (:score (get @best selection-metric))) (reset! best (assoc-in @best [selection-metric] {:window-size window-size :vector-size vector-size :walk-length walk-length :walks-per-vertex walks-per-vertex :angle angle :score score})))))))))))) @best))
(svm-grid-search graph :grid-parameters {:window-size [10 15 20] :vector-size [64 128 256] :walk-length [5 10 15] :walks-per-vertex [32 64 128] :angle [60 90 120] :selection-metrics [:precision :accuracy :recall :f1]})
{:precision
{:window-size 10,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 60,
:score 0.6812866},
:accuracy
{:window-size 10,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 0.676259},
:recall
{:window-size 10,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 0.99640286},
:f1
{:window-size 10,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 0.80406386}}
For the same first-sense-context disambiguation algorithm, once the key hyperparameters of the pipeline are optimized, then we endup with a F1 score of 0.8040, which is an increase of 46.72% over the baseline. Recall has now increased by 99.52%, accuracy increased by 60.73% and precision increased by 12.04%.
Still, understand that when performing the grid search in this manner that many of the hyperparameters we are trying to optimize are related to the DeepWalk algorithm. Because of the nature of the algorithm (when the model is trained, the paths are randomly created and the learning starts with random seeds) we can't reproduce exactly the same results every time we re-create a DeepWalk instance. However the results tend to be similar with a differences of +/- 0.02 for most of the metrics.
Depending on the task at hand we don't necessarly want to keep the hyperparameters of the best score. If model creation and execution speed is also a governing consideration, we may want to sacrifice 0.03 of the F1 score to have the :window-size, :vector-size, :walk-length and :walk-per-vertex as small as possible.
But in any case, these numbers indicate the kind of performances we may expect from this disambiguation process.
(def deep-walk (create-deep-walk graph :window-size 10 :vector-size 128 :learning-rate 0.025)) (train deep-walk graph 10 128) (binding [vertex-vectors (.getVertexVectors (.lookupTable deep-walk))] (evaluate-disambiguation-model "resources/disambiguation-gold.standard.csv" :max-angle 150))
True positive: 229
false positive: 123
True negative: 5
False negative: 1
Precision: 0.6505682
Recall: 0.9956522
Accuracy: 0.65363127
F1: 0.7869416
Different Sliding Window Strategies
Another part of this disambiguation process that has an impact on results is how the "context" of a word is being created. There are multiple ways to define a context, such as extending the window size or letting window size extend over sentence boundaries. For clarity's sake, we initially defined the context 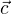as:
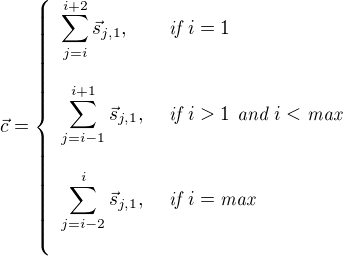
One of the issues with this definition of "context" is that, so far,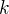 
(the senses for each word) is always 1, which means that the context is always defined with the first sense of a word, whatever it is. This is why we called this method the first-sense-context disambiguation. Biasing the context to the first sense ignores the other senses that may be summed into the context vector. However, this initial definition is simple enough and, as we saw above, we still have adequate results with it. Still, what could be other strategies?
Ignore Target Word Senses In Context
The first test we may do is to remove the target word's sense (the word we are trying to disambiguate) from the context. That way, we would make sure that we don't bias the context toward that sense. The context would be defined as:
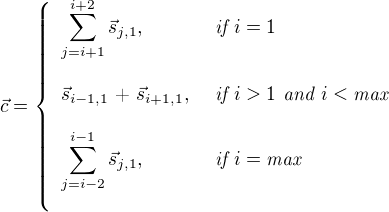
We are still picking the first sense of each word that belongs to the context, but we are not considering that sense for the target word when we calculate the context vector. Let's see what is the impact of changing the context with this new definition. To test this new context, we have to change the (get-context) function to reflect the new machanism and to re-test and re-optimize the hyperparameters.
(defn get-context [i tags] (if (= (count tags) 1) ;; There is only one tag in the sentence (get-first-sense-vector (last (first tags))) (if (= (count tags) 2) ;; There is only 2 tags in the sentence (if (= i 0) (sum-vectors (get-first-sense-vector (last (second tags)))) (sum-vectors (get-first-sense-vector (last (first tags))))) ;; Target concept is the first one of the sentence (if (= i 0) (sum-vectors (get-first-sense-vector (last (second tags))) (get-first-sense-vector (last (nth tags (+ i 2))))) ;; Target concept is the last one of the sentence (if (= i (- (count tags) 1)) (sum-vectors (get-first-sense-vector (last (nth tags (- i 2)))) (get-first-sense-vector (last (nth tags (- i 1))))) ;; Target is in-between (sum-vectors (get-first-sense-vector (last (nth tags (- i 1)))) (get-first-sense-vector (last (nth tags (+ i 1))))))))))
Now let's re-optimize and re-evaluate the impact of this modification on our gold standard:
(svm-grid-search graph :grid-parameters {:window-size [10 15 20] :vector-size [64 128 256] :walk-length [5 10 15] :walks-per-vertex [32 64 128] :angle [60 90 120] :selection-metrics [:precision :accuracy :recall :f1]})
{:precision
{:window-size 20,
:vector-size 128,
:walk-length 5,
:walks-per-vertex 32,
:angle 120,
:score 0.6666667},
:accuracy
{:window-size 20,
:vector-size 128,
:walk-length 5,
:walks-per-vertex 32,
:angle 120,
:score 0.66906476},
:recall
{:window-size 20,
:vector-size 128,
:walk-length 5,
:walks-per-vertex 32,
:angle 120,
:score 0.99636364},
:f1
{:window-size 20,
:vector-size 128,
:walk-length 5,
:walks-per-vertex 32,
:angle 120,
:score 0.79883385}}
With this modification to the context creation algorithm, every metric slightly dropped compared to our previous version of the first-sense disambiguation algorithm. However, this modification of the algorithm has little impact on the final results if we consider the margin of error we have for the F1 score incurred by DeepWalk's random walks and training process.
(def deep-walk (create-deep-walk graph :window-size 15 :vector-size 128 :learning-rate 0.025)) (train deep-walk graph 15 128) (binding [vertex-vectors (.getVertexVectors (.lookupTable deep-walk))] (evaluate-disambiguation-model "resources/disambiguation-gold.standard.csv" :max-angle 120))
Consider Multiple Contexts
Another modification we will test is to define not a single context but multiple contexts and to keep the most relevant one. So far, we only used the top sense for each word to define the context. The truth is that most of the words have multiple possible senses, which means that we are currently ignoring them. Let's again revisit our initial example:
If the target word is buildings then the contexts we created so far only considered the senses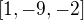 
, 
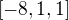and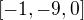 
but what about the other two? What we want to do here is to create multiple contexts and then to compare each of the senses of the target word against each of these contexts. Then we will check the angle between each of the senses of the target word against each of the contexts. Then we will keep the sense that is most closely related to one of the context vectors.
The contexts are simply created out of all the possible combinations between each of the senses of each words within the window. With the example above, the possible combinations are:
(for [x [[1 -9 -2] [2 3 -7]] y [[-8 1 1]] z [[-1 -9 0] [0 3 -1]]] (clojure.pprint/pprint (vector x y x)))
[[1 -9 -2] [-8 1 1] [1 -9 -2]]
[[1 -9 -2] [-8 1 1] [1 -9 -2]]
[[2 3 -7] [-8 1 1] [2 3 -7]]
[[2 3 -7] [-8 1 1] [2 3 -7]]
To now compare this larger number of combinations, we need to modify the evaluation procedure. We have to modify how the contexts are created and how all possible contexts are generated. Then we have to modify how we predict the label for an example by using the most relevant context.
(defn disambiguate [line] (let [tags (re-seq #"\[\[(.*?)\]\]\(\((.*?)\)\)" line)] (loop [i 0 tag (first tags) rtags (rest tags)] (let [word (second tag) concepts (last tag) concept (get-tag-concept concepts)] (println word " --> " concepts) ;; Disambiguate concepts (let [ambiguous-concepts (string/split (first (string/split concepts #"::")) #" ")] (doseq [ambiguous-concept ambiguous-concepts] ;; (println "a-vector: " (get-vector ambiguous-concept)) (let [unambiguous (first (->> (get-contexts i tags) (map (fn [context] {(angle (get-vector ambiguous-concept) context) ambiguous-concept})) (apply merge) sort))] ;; (println "b-vector: " (get-context i tags)) (println "Unambiguous concept: " (second unambiguous)) (println "angle: " (first unambiguous)) (println))))) (when-not (empty? rtags) (recur (inc i) (first rtags) (rest rtags))))))
(require '[clojure.math.combinatorics :as combo]) (defn get-word-senses [i tags] (let [senses (last (nth tags i))] (if (> (.indexOf senses "::") -1) (string/split (second (re-find #"(.*)::" senses)) #" ") senses))) (defn get-contexts [i tags] (if (= (count tags) 1) ;; There is only one tag in the sentence (get-first-sense-vector (last (first tags))) (if (= (count tags) 2) ;; There is only 2 tags in the sentence (let [contexts (combo/cartesian-product (get-word-senses 0 tags) (get-word-senses 1 tags))] (->> contexts (mapv (fn [context] (sum-vectors (get-first-sense-vector (first context)) (get-first-sense-vector (second context))))))) ;; Target concept is the first one of the sentence (if (= i 0) (let [contexts (combo/cartesian-product (get-word-senses 0 tags) (get-word-senses 1 tags) (get-word-senses 2 tags))] (->> contexts (mapv (fn [context] (sum-vectors (get-first-sense-vector (first context)) (get-first-sense-vector (second context)) (get-first-sense-vector (nth context 2))))))) ;; Target concept is the last one of the sentence (if (= i (- (count tags) 1)) (let [contexts (combo/cartesian-product (get-word-senses (- i 2) tags) (get-word-senses (- i 1) tags) (get-word-senses i tags))] (->> contexts (mapv (fn [context] (sum-vectors (get-first-sense-vector (first context)) (get-first-sense-vector (second context)) (get-first-sense-vector (nth context 2))))))) ;; Target is in-between (let [contexts (combo/cartesian-product (get-word-senses (- i 1) tags) (get-word-senses i tags) (get-word-senses (+ i 1) tags))] (->> contexts (mapv (fn [context] (sum-vectors (get-first-sense-vector (first context)) (get-first-sense-vector (second context)) (get-first-sense-vector (nth context 2)))))))))))) (defn predict-label [ambiguous-concepts i tags max-angle] (second (first (->> ambiguous-concepts (map (fn [ambiguous-concept] (let [unambiguous (first (->> (get-contexts i tags) (map (fn [context] (if-let [a (get-vector ambiguous-concept)] (if-not (nil? context) (if (> (angle a context) max-angle) {} {(angle a context) ambiguous-concept}) {}) {}))) (apply merge) sort))] {(first unambiguous) (second unambiguous)}))) (apply merge) sort)))) (defn predict-label-angle [ambiguous-concepts i tags] (first (->> ambiguous-concepts (map (fn [ambiguous-concept] (let [unambiguous (first (->> (get-contexts i tags) (map (fn [context] (if-let [a (get-vector ambiguous-concept)] (if-not (nil? context) {(angle a context) ambiguous-concept} {}) {}))) (apply merge) sort))] {(first unambiguous) (second unambiguous)}))) (apply merge) sort)))
Now, using this changed disambiguation method, let's optimize the hyperparameters of the pipeline to see how this method can perform compared to the baseline.
(svm-grid-search graph :grid-parameters {:window-size [10 15 20] :vector-size [64 128 256] :walk-length [5 10 15] :walks-per-vertex [32 64 128] :angle [60 90 120] :selection-metrics [:precision :accuracy :recall :f1]})
{:precision
{:window-size 15,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 60,
:score 0.69970846},
:accuracy
{:window-size 15,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 0.676259},
:recall
{:window-size 15,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 0.98566306},
:f1
{:window-size 15,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 0.8029197}}
These results are nearly the same as the first-sense-context method described above. Our first intuition is that this more complicated method may have little or no impact on the overall performance. Yet, as we will see below, this is actually not the case in all situations.
(def deep-walk (create-deep-walk graph :window-size 15 :vector-size 128 :learning-rate 0.025)) (train deep-walk graph 15 128) (binding [vertex-vectors (.getVertexVectors (.lookupTable deep-walk))] (evaluate-disambiguation-model "resources/disambiguation-gold.standard.csv" :max-angle 120))
Focus Evaluation Of Multiple Senses
Now that we evaluated how different strategies perform on the entire gold standard, what we will do next is to evaluate how the different strategies perform when we only focus on the example that has multiple possible senses. To run this evaluation, we will modify the (evaluate-disambiguation-model) function such that we only predict the disambiguated word sense when multiple senses have been tagged for that word.
(defn evaluate-disambiguation-model [gold-standard-file & {:keys [max-angle] :or {max-angle 90.0}}] (let [sentences (with-open [in-file (io/reader gold-standard-file)] (doall (csv/read-csv in-file :separator \tab))) true-positive (atom 0) false-positive (atom 0) true-negative (atom 0) false-negative (atom 0)] (doseq [[sentence] sentences] (let [tags (re-seq #"\[\[(.*?)\]\]\(\((.*?)\)\)" sentence)] (loop [i 0 tag (first tags) rtags (rest tags)] (when-not (= i (count tags)) ;; Disambiguate concepts (let [word (second tag) concepts (last tag) concept (get-tag-concept concepts) label (second (re-find #"::(.*)" concepts)) ambiguous-concepts (string/split (first (string/split concepts #"::")) #" ")] (when (> (count ambiguous-concepts) 1) (let [predicted-label (predict-label ambiguous-concepts i tags max-angle)] (when (and (= label predicted-label) (not (empty? label)) (not (empty? predicted-label))) (swap! true-positive inc)) (when (and (not (= label predicted-label)) (not (empty? predicted-label))) (swap! false-positive inc)) (when (and (empty? label) (empty? predicted-label)) (swap! true-negative inc)) (when (and (not (empty? label)) (empty? predicted-label)) (swap! false-negative inc)))) (recur (inc i) (first rtags) (rest rtags))))))) (println "True positive: " @true-positive) (println "false positive: " @false-positive) (println "True negative: " @true-negative) (println "False negative: " @false-negative) (println) (if (= 0 @true-positive) (let [precision 0 recall 0 accuracy 0 f1 0] (println "Precision: " precision) (println "Recall: " recall) (println "Accuracy: " accuracy) (println "F1: " f1) {:precision precision :recall recall :accuracy accuracy :f1 f1}) (let [precision (float (/ @true-positive (+ @true-positive @false-positive))) recall (float (/ @true-positive (+ @true-positive @false-negative))) accuracy (float (/ (+ @true-positive @true-negative) (+ @true-positive @false-negative @false-positive @true-negative))) f1 (float (* 2 (/ (* precision recall) (+ precision recall))))] (println "Precision: " precision) (println "Recall: " recall) (println "Accuracy: " accuracy) (println "F1: " f1) {:precision precision :recall recall :accuracy accuracy :f1 f1}))))
Evaluation At Random
To put the next evaluations into context, the first thing we will do is to check what would be the score for each metric if we would pick the concept at random. What we do is to modify the (evaluate-disambiguation-model) function to take the "disambiguated" concept at random. Then we run that evaluation one thousand times and display the average of these runs for each metric. This will give us the foundation to evaluate the performance of each of the strategies below.
(defn evaluate-disambiguation-model-random [gold-standard-file & {:keys [max-angle] :or {max-angle 90.0}}] (let [sentences (with-open [in-file (io/reader gold-standard-file)] (doall (csv/read-csv in-file :separator \tab))) true-positive (atom 0) false-positive (atom 0) true-negative (atom 0) false-negative (atom 0)] (doseq [[sentence] sentences] (let [tags (re-seq #"\[\[(.*?)\]\]\(\((.*?)\)\)" sentence)] (loop [i 0 tag (first tags) rtags (rest tags)] (when-not (= i (count tags)) ;; Disambiguate concepts (let [word (second tag) concepts (last tag) concept (get-tag-concept concepts) label (second (re-find #"::(.*)" concepts)) ambiguous-concepts (string/split (first (string/split concepts #"::")) #" ")] (when (> (count ambiguous-concepts) 1) (let [predicted-label (rand-nth (into ambiguous-concepts [nil]))] (when (and (= label predicted-label) (not (empty? label)) (not (empty? predicted-label))) (swap! true-positive inc)) (when (and (not (= label predicted-label)) (not (empty? predicted-label))) (swap! false-positive inc)) (when (and (empty? label) (empty? predicted-label)) (swap! true-negative inc)) (when (and (not (empty? label)) (empty? predicted-label)) (swap! false-negative inc)))) (recur (inc i) (first rtags) (rest rtags))))))) (if (= 0 @true-positive) (let [precision 0 recall 0 accuracy 0 f1 0] {:precision precision :recall recall :accuracy accuracy :f1 f1}) (let [precision (float (/ @true-positive (+ @true-positive @false-positive))) recall (float (/ @true-positive (+ @true-positive @false-negative))) accuracy (float (/ (+ @true-positive @true-negative) (+ @true-positive @false-negative @false-positive @true-negative))) f1 (float (* 2 (/ (* precision recall) (+ precision recall))))] {:precision precision :recall recall :accuracy accuracy :f1 f1}))))
(let [f1 (atom 0) precision (atom 0) recall (atom 0) accuracy (atom 0) nb (atom 0)] (dotimes [i 1000] (let [results (evaluate-disambiguation-model-random "resources/disambiguation-gold.standard.csv")] (swap! nb inc) (swap! f1 + (:f1 results)) (swap! precision + (:precision results)) (swap! recall + (:recall results)) (swap! accuracy + (:accuracy results)))) (println "Average precision: " (/ @precision @nb)) (println "Average recall: " (/ @recall @nb)) (println "Average accuracy: " (/ @accuracy @nb)) (println "Average F1: " (/ @f1 @nb)))
Average precision: 0.3583671303540468
Average recall: 0.4984975547492504
Average accuracy: 0.295875000089407
Average F1: 0.4158918097615242
This gives us a baseline precision score of 0.358, recall score of 0.498, accuracy score of 0.295 and F1 score of 0.4158. As we can notice if we compare with the random baseline with the full gold standard is that when we focus on the words which have multiple possible senses, the problem becomes much harder.
Evaluation Using First Sense Context
(svm-grid-search graph :grid-parameters {:window-size [10 15 20] :vector-size [64 128 256] :walk-length [5 10 15] :walks-per-vertex [32 64 128] :angle [60 90 120] :selection-metrics [:precision :accuracy :recall :f1]})
{:precision
{:window-size 15,
:vector-size 128,
:walk-length 5,
:walks-per-vertex 32,
:angle 60,
:score 0.4397163},
:accuracy
{:window-size 15,
:vector-size 256,
:walk-length 5,
:walks-per-vertex 32,
:angle 60,
:score 0.41875},
:recall
{:window-size 10,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 1.0},
:f1
{:window-size 15,
:vector-size 256,
:walk-length 5,
:walks-per-vertex 32,
:angle 60,
:score 0.58295965}}
For the same first-sense-context disambiguation algorithm, once the key hyperparameters of the pipeline are optimized,
then we endup with a F1 score of 0.5829 which is an increase of 40.19% over the baseline. Recall increases by
100.64%, accuracy increases by 41.55% and precision increases by 22.72%.
Evaluation Without Target Word's Senses
Now let's re-run the procedure when we don't focus on the target word that we want to disambiguate to create the context vector.
(svm-grid-search graph :grid-parameters {:window-size [10 15 20] :vector-size [64 128 256] :walk-length [5 10 15] :walks-per-vertex [32 64 128] :angle [60 90 120] :selection-metrics [:precision :accuracy :recall :f1]})
{:precision
{:window-size 10,
:vector-size 128,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 0.38931298},
:accuracy
{:window-size 10,
:vector-size 128,
:walk-length 5,
:walks-per-vertex 32,
:angle 120,
:score 0.38125},
:recall
{:window-size 10,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 120,
:score 1.0},
:f1
{:window-size 10,
:vector-size 128,
:walk-length 5,
:walks-per-vertex 32,
:angle 120,
:score 0.55203617}}
In this case, the F1 score increased by 32.76% over the baseline. Recall increases by 238.07%, accuracy increases by 28.87% and precision increases by 8.65%. Like we experienced previously, all of the results decreased compared to the version of the algorithm that included the sense of the target word in the calculation of the context vector. This option is not improving matters, and should be dropped from further consideration.
Evaluation With Multiple Contexts
Finally let's evaluate the other modification we did that keeps the context vector that best matches one of the senses for the target word.
(svm-grid-search graph :grid-parameters {:window-size [10 15 20] :vector-size [64 128 256] :walk-length [5 10 15] :walks-per-vertex [32 64 128] :angle [60 90 120] :selection-metrics [:precision :accuracy :recall :f1]})
{:precision
{:window-size 15,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 60,
:score 0.4566929},
:accuracy
{:window-size 15,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 0.44375},
:recall
{:window-size 15,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 0.9583333},
:f1
{:window-size 15,
:vector-size 64,
:walk-length 5,
:walks-per-vertex 32,
:angle 90,
:score 0.6079295}}
In this case, the F1 score increased by 46.2% over the baseline. Recall increases by 223.97%, accuracy increases by 50%, and precision increases by 27.44%. Except for the recall, all the other metrics improved compared to the first-sense-context method. Though we previously found that there were no apparent improvements using this method against using the first-sense-context algorithm, when we look at the words that have multiple senses only, we see that there is a clear improvement on all the metrics except for the recall, which is slightly lower. This suggests that in a situation where multiple words have multiple possible senses, then this method should outperform the first-sense-context one.
Conclusion
Disambiguating tagged concepts from a knowledge graph such as KBpedia is not an easy task. However, if a coherent and consistent knowledge graph such as KBpedia is used as the starting point, along with existing machine learning algorithms such as DeepWalk, it is possible to obtain good disambiguation performance in a short period of time without the need to create extensive training sets.
With the tests we performed in this article, we gained insight into the kinds of things that may have much influence on the disambiguation process. We also learned how different strategies could be tested to get the best results for a specific disambiguation task.
Results from these disambiguation processes can easily become the input into other tasks such as a document classification. [Disambiguated], tagged concepts should be a better basis for classifying the documents. If the concepts are not disambiguated, then much noise is added, leading to lower performance of the classification task.
There are two main advantages of using such a disambiguation system. The first advantage is that we have no need to create any kind of training set, which would obviously be quite expensive to create considering that hundreds of contexts for each concept within the knowledge graph would need to be disambiguated manually. With a knowledge graph of the size of KBpedia, that would mean a training set of about 3.8 million examples. But since the training takes place on the structure of the knowledge graph that already exists, there is no need to create such a training set. Also, different parts of the knowledge graph could be used to create different kinds of knowledge structures ([i.e.], in this article we used the sub-class-of paths within the knowledge structure, but we could have used different aspects, different relationship paths, etc.). Alternate knowledge structures may result in different graph embeddings that may perform better in different situations.
The second advantage is that since we only use simple linear algebra to disambiguate the concepts, performance is really fast. On average, we can disambiguate a single word within 0.65 milliseconds which means that we can disambiguate about 1,538 words per second with this method on a commodity desktop computer.
Many more experiments could be performed to increase the performance of these methods, while retaining the ease of model creation and the disambiguation speed. New context algorithms could be tested, bigger sliding windows, etc. New graph embedding creation algorithms could be tested. New DeepWalk graph walk algorithms could be used such as breadth and depth first searches, etc.
Footnotes
|
|
KBpedia |
KBpedia exploits large-scale knowledge bases and semantic technologies for machine learning, data interoperability and mapping, and fact extraction and tagging.
Latest News
- KBpedia Adds Major eCommerce Capabilities 06/15/2020
- KBpedia Continues Quality Improvements 12/04/2019
- Wikidata Coverage Nearly Complete (98%) 04/08/2019
Other Resources
Contact Us
380 Knowling Drive
Coralville, IA 52241
U.S.A.
Voice: +1 319 621 5225
2016-2022 © Michael K. Bergman. All Rights Reserved.